
This chapter provides a complete reference for all sequential (i.e.,
one-processor) FFTW functions. We first define the data types upon
which FFTW operates, that is, real, complex, and "halfcomplex" numbers
(see Section Data Types). Then, in four sections, we explain the FFTW
program interface for complex one-dimensional transforms
(see Section One-dimensional Transforms Reference), complex
multi-dimensional transforms (see Section Multi-dimensional Transforms Reference), and real one-dimensional transforms (see Section Real One-dimensional Transforms Reference), real multi-dimensional
transforms (see Section Real Multi-dimensional Transforms Reference).
Section Wisdom Reference describes the wisdom mechanism for
exporting and importing plans. Finally, Section Memory Allocator Reference describes how to change FFTW's default memory allocator.
For parallel transforms, See Section Parallel FFTW.
The routines in the FFTW package use three main kinds of data types. Real and complex numbers should be already known to the reader. We also use the term halfcomplex to describe complex arrays in a special packed format used by the one-dimensional real transforms (taking advantage of the hermitian symmetry that arises in those cases).
By including <fftw.h> or <rfftw.h>, you will have access
to the following definitions:
typedef double fftw_real;
typedef struct {
fftw_real re, im;
} fftw_complex;
#define c_re(c) ((c).re)
#define c_im(c) ((c).im)
All FFTW operations are performed on the fftw_real and
fftw_complex data types. For fftw_complex numbers, the
two macros c_re and c_im retrieve, respectively, the real
and imaginary parts of the number.
A real array is an array of real numbers. A complex array is an array of complex numbers. A one-dimensional array X of n complex numbers is hermitian if the following property holds: for all 0 <= i < n, we have Xi = conj(Xn-i)}. Hermitian arrays are relevant to FFTW because the Fourier transform of a real array is hermitian.
Because of its symmetry, a hermitian array can be stored in half the
space of a complex array of the same size. FFTW's one-dimensional real
transforms store hermitian arrays as halfcomplex arrays. A
halfcomplex array of size n is
a one-dimensional array of n fftw_real numbers. A
hermitian array X in stored into a halfcomplex array Y as
follows.
For all integers i such that 0 <= i <= n / 2, we have
Yi = Re(Xi). For all integers i such that 0
< i < n / 2, we have Yn-i = Im(Xi).
We now illustrate halfcomplex storage for n = 4 and n = 5, since the scheme depends on the parity of n. Let n = 4. In this case, we have Y0 = Re(X0), Y1 = Re(X1), Y2 = Re(X2), and Y3 = Im(X1). Let now n = 5. In this case, we have Y0 = Re(X0), Y1 = Re(X1), Y2 = Re(X2), Y3 = Im(X2), and Y4 = Im(X1).
By default, the type fftw_real equals the C type double.
To work in single precision rather than double precision, #define
the symbol FFTW_ENABLE_FLOAT in fftw.h and then recompile
the library. On Unix systems, you can instead use configure
--enable-float at installation time (see Section Installation and Customization).
In version 1 of FFTW, the data types were called FFTW_REAL and
FFTW_COMPLEX. We changed the capitalization for consistency with
the rest of FFTW's conventions. The old names are still supported, but
their use is deprecated.
The one-dimensional complex routines are generally prefixed with
fftw_. Programs using FFTW should be linked with -lfftw
-lm on Unix systems, or with the FFTW and standard math libraries in
general.
#include <fftw.h>
fftw_plan fftw_create_plan(int n, fftw_direction dir,
int flags);
fftw_plan fftw_create_plan_specific(int n, fftw_direction dir,
int flags,
fftw_complex *in, int istride,
fftw_complex *out, int ostride);
The function fftw_create_plan creates a plan, which is
a data structure containing all the information that fftw
needs in order to compute the 1D Fourier transform. You can
create as many plans as you need, but only one plan for a given
array size is required (a plan can be reused many times).
fftw_create_plan returns a valid plan, or NULL
if, for some reason, the plan can't be created. In the
default installation, this cannot happen, but it is possible
to configure FFTW in such a way that some input sizes are
forbidden, and FFTW cannot create a plan.
The fftw_create_plan_specific variant takes as additional
arguments specific input/output arrays and their strides. For the last
four arguments, you should pass the arrays and strides that you will
eventually be passing to fftw. The resulting plans will be
optimized for those arrays and strides, although they may be used on
other arrays as well. Note: the contents of the in and out arrays are
destroyed by the specific planner (the initial contents are
ignored, so the arrays need not have been initialized).
n is the size of the transform. It can be
any positive integer.
dir is the sign of the exponent in the formula that
defines the Fourier transform. It can be -1 or +1.
The aliases FFTW_FORWARD and FFTW_BACKWARD
are provided, where FFTW_FORWARD stands for -1.
flags is a boolean OR (`|') of zero or more of the following:
FFTW_MEASURE: this flag tells FFTW to find the optimal plan by
actually computing several FFTs and measuring their
execution time. Depending on the installation, this can take some
time. (2)
FFTW_ESTIMATE: do not run any FFT and provide a "reasonable"
plan (for a RISC processor with many registers). If neither
FFTW_ESTIMATE nor FFTW_MEASURE is provided, the default is
FFTW_ESTIMATE.
FFTW_OUT_OF_PLACE: produce a plan assuming that the input and
output arrays will be distinct (this is the default).
FFTW_IN_PLACE: produce a plan assuming that you want the output
in the input array. The algorithm used is not necessarily in place:
FFTW is able to compute true in-place transforms only for small values
of n. If FFTW is not able to compute the transform in-place, it
will allocate a temporary array (unless you provide one yourself),
compute the transform out of place, and copy the result back.
Warning: This option changes the meaning of some parameters of
fftw (see Section Computing the One-dimensional Transform).
The in-place option is mainly provided for people who want to write
their own in-place multi-dimensional Fourier transform, using FFTW as a
base. For example, consider a three-dimensional n * n * n
transform. An out-of-place algorithm will need another array (which may
be huge). However, FFTW can compute the in-place transform along
each dimension using only a temporary array of size n.
Moreover, if FFTW happens to be able to compute the transform truly
in-place, no temporary array and no copying are needed. As distributed,
FFTW `knows' how to compute in-place transforms of size 1, 2, 3, 4, 5, 6,
7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 32 and 64.
The default mode of operation is FFTW_OUT_OF_PLACE.
FFTW_USE_WISDOM: use any wisdom that is available to help
in the creation of the plan. (See Section Words of Wisdom.)
This can greatly speed the creation of plans, especially with the
FFTW_MEASURE option. FFTW_ESTIMATE plans can also take
advantage of wisdom to produce a more optimal plan (based on past
measurements) than the estimation heuristic would normally
generate. When the FFTW_MEASURE option is used, new wisdom
will also be generated if the current transform size is not completely
understood by existing wisdom.
in, out, istride, ostride (only for
fftw_create_plan_specific): see corresponding arguments in the
description of fftw. (See Section Computing the One-dimensional Transform.) In particular, the out and ostride
parameters have the same special meaning for FFTW_IN_PLACE
transforms as they have for fftw.
We recommend the use of the specific planners, even in cases where you will be transforming arrays different from those passed to the specific planners, as they confer the following advantages:
N) temporary storage, where N is
the maximum dimension, while it is creating the plan.)
On the other hand, note that the specific planner destroys the
contents of the in and out arrays.
#include <fftw.h>
void fftw(fftw_plan plan, int howmany,
fftw_complex *in, int istride, int idist,
fftw_complex *out, int ostride, int odist);
void fftw_one(fftw_plan plan, fftw_complex *in,
fftw_complex *out);
The function fftw computes the one-dimensional Fourier transform,
using a plan created by fftw_create_plan (See Section Plan Creation for One-dimensional Transforms.) The function
fftw_one provides a simplified interface for the common case of
single input array of stride 1.
plan is the plan created by fftw_create_plan
(see Section Plan Creation for One-dimensional Transforms).
howmany is the number of transforms fftw will compute.
It is faster to tell FFTW to compute many transforms, instead of
simply calling fftw many times.
in, istride and idist describe the input array(s).
There are howmany input arrays; the first one is pointed to by
in, the second one is pointed to by in + idist, and so on,
up to in + (howmany - 1) * idist. Each input array consists of
complex numbers (see Section Data Types), which are not necessarily
contiguous in memory. Specifically, in[0] is the first element
of the first array, in[istride] is the second element of the
first array, and so on. In general, the i-th element of the
j-th input array will be in position in[i * istride + j *
idist].
out, ostride and odist describe the output
array(s). The format is the same as for the input array.
plan specifies an in-place transform, ostride and
odist are always ignored. If out is NULL,
out is ignored, too. Otherwise, out is interpreted as a
pointer to an array of n complex numbers, that FFTW will use as
temporary space to perform the in-place computation. out is used
as scratch space and its contents destroyed. In this case, out
must be an ordinary array whose elements are contiguous in memory (no
striding).
The function fftw_one transforms a single, contiguous input array
to a contiguous output array. By definition, the call
fftw_one(plan, in, out)
is equivalent to
fftw(plan, 1, in, 1, 0, out, 1, 0)
#include <fftw.h> void fftw_destroy_plan(fftw_plan plan);
The function fftw_destroy_plan frees the plan plan and
releases all the memory associated with it. After destruction, a plan
is no longer valid.
In this section, we define precisely what FFTW computes. Please be warned that different authors and software packages might employ different conventions than FFTW does.
The forward transform of a complex array X of size n computes an array Y, where

The backward transform computes
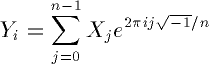
FFTW computes an unnormalized transform, that is, the equation IFFT(FFT(X)) = n X holds. In other words, applying the forward and then the backward transform will multiply the input by n.
An FFTW_FORWARD transform corresponds to a sign of -1 in
the exponent of the DFT. Note also that we use the standard
"in-order" output ordering--the k-th output corresponds to the
frequency k/n (or k/T, where T is your total
sampling period). For those who like to think in terms of positive and
negative frequencies, this means that the positive frequencies are
stored in the first half of the output and the negative frequencies are
stored in backwards order in the second half of the output. (The
frequency -k/n is the same as the frequency (n-k)/n.)
The multi-dimensional complex routines are generally prefixed with
fftwnd_. Programs using FFTWND should be linked with -lfftw
-lm on Unix systems, or with the FFTW and standard math libraries in
general.
#include <fftw.h>
fftwnd_plan fftwnd_create_plan(int rank, const int *n,
fftw_direction dir, int flags);
fftwnd_plan fftw2d_create_plan(int nx, int ny,
fftw_direction dir, int flags);
fftwnd_plan fftw3d_create_plan(int nx, int ny, int nz,
fftw_direction dir, int flags);
fftwnd_plan fftwnd_create_plan_specific(int rank, const int *n,
fftw_direction dir,
int flags,
fftw_complex *in, int istride,
fftw_complex *out, int ostride);
fftwnd_plan fftw2d_create_plan_specific(int nx, int ny,
fftw_direction dir,
int flags,
fftw_complex *in, int istride,
fftw_complex *out, int ostride);
fftwnd_plan fftw3d_create_plan_specific(int nx, int ny, int nz,
fftw_direction dir, int flags,
fftw_complex *in, int istride,
fftw_complex *out, int ostride);
The function fftwnd_create_plan creates a plan, which is a data
structure containing all the information that fftwnd needs in
order to compute a multi-dimensional Fourier transform. You can create
as many plans as you need, but only one plan for a given array size is
required (a plan can be reused many times). The functions
fftw2d_create_plan and fftw3d_create_plan are optional,
alternative interfaces to fftwnd_create_plan for two and three
dimensions, respectively.
fftwnd_create_plan returns a valid plan, or NULL if, for
some reason, the plan can't be created. This can happen if memory runs
out or if the arguments are invalid in some way (e.g. if rank <
0).
The create_plan_specific variants take as additional arguments
specific input/output arrays and their strides. For the last four
arguments, you should pass the arrays and strides that you will
eventually be passing to fftwnd. The resulting plans will be
optimized for those arrays and strides, although they may be used on
other arrays as well. Note: the contents of the in and out arrays are
destroyed by the specific planner (the initial contents are
ignored, so the arrays need not have been initialized).
See Section Discussion on Specific Plans, for a discussion on specific plans.
rank is the dimensionality of the arrays to be transformed. It
can be any non-negative integer.
n is a pointer to an array of rank integers, giving the
size of each dimension of the arrays to be transformed. These sizes,
which must be positive integers, correspond to the dimensions of
row-major arrays--i.e. n[0] is the size of the dimension whose
indices vary most slowly, and so on. (See Section Multi-dimensional Array Format, for more information on row-major storage.)
See Section Plan Creation for One-dimensional Transforms,
for more information regarding optimal array sizes.
nx and ny in fftw2d_create_plan are positive
integers specifying the dimensions of the rank 2 array to be
transformed. i.e. they specify that the transform will operate on
nx x ny arrays in row-major order, where nx is the number
of rows and ny is the number of columns.
nx, ny and nz in fftw3d_create_plan are
positive integers specifying the dimensions of the rank 3 array to be
transformed. i.e. they specify that the transform will operate on
nx x ny x nz arrays in row-major order.
dir is the sign of the exponent in the formula that defines the
Fourier transform. It can be -1 or +1. The aliases
FFTW_FORWARD and FFTW_BACKWARD are provided, where
FFTW_FORWARD stands for -1.
flags is a boolean OR (`|') of zero or more of the following:
FFTW_MEASURE: this flag tells FFTW to find the optimal plan by
actually computing several FFTs and measuring their execution
time.
FFTW_ESTIMATE: do not run any FFT and provide a "reasonable"
plan (for a RISC processor with many registers). If neither
FFTW_ESTIMATE nor FFTW_MEASURE is provided, the default is
FFTW_ESTIMATE.
FFTW_OUT_OF_PLACE: produce a plan assuming that the input
and output arrays will be distinct (this is the default).
FFTW_IN_PLACE: produce a plan assuming that you want to perform
the transform in-place. (Unlike the one-dimensional transform, this
"really" (3) performs the
transform in-place.) Note that, if you want to perform in-place
transforms, you must use a plan created with this option.
The default mode of operation is FFTW_OUT_OF_PLACE.
FFTW_USE_WISDOM: use any wisdom that is available to help
in the creation of the plan. (See Section Words of Wisdom.) This can greatly
speed the creation of plans, especially with the FFTW_MEASURE
option. FFTW_ESTIMATE plans can also take advantage of
wisdom to produce a more optimal plan (based on past
measurements) than the estimation heuristic would normally
generate. When the FFTW_MEASURE option is used, new wisdom
will also be generated if the current transform size is not completely
understood by existing wisdom. Note that the same wisdom
is shared between one-dimensional and multi-dimensional transforms.
in, out, istride, ostride (only for the
_create_plan_specific variants): see corresponding arguments in
the description of fftwnd. (See Section Computing the Multi-dimensional Transform.)
#include <fftw.h>
void fftwnd(fftwnd_plan plan, int howmany,
fftw_complex *in, int istride, int idist,
fftw_complex *out, int ostride, int odist);
void fftwnd_one(fftwnd_plan p, fftw_complex *in,
fftw_complex *out);
The function fftwnd computes one or more multi-dimensional
Fourier Transforms, using a plan created by fftwnd_create_plan
(see Section Plan Creation for Multi-dimensional Transforms). (Note that the plan determines the rank and dimensions of
the array to be transformed.) The function fftwnd_one provides a
simplified interface for the common case of single input array of stride
1.
plan is the plan created by fftwnd_create_plan.
(see Section Plan Creation for Multi-dimensional Transforms). In the case of two and three-dimensional transforms, it
could also have been created by fftw2d_create_plan or
fftw3d_create_plan, respectively.
howmany is the number of multi-dimensional transforms
fftwnd will compute.
in, istride and idist describe the input array(s).
There are howmany multi-dimensional input arrays; the first one
is pointed to by in, the second one is pointed to by in +
idist, and so on, up to in + (howmany - 1) * idist. Each
multi-dimensional input array consists of complex numbers (see Section Data Types), stored in row-major format (see Section Multi-dimensional Array Format), which are not necessarily contiguous in memory. Specifically,
in[0] is the first element of the first array, in[istride]
is the second element of the first array, and so on. In general, the
i-th element of the j-th input array will be in position
in[i * istride + j * idist]. Note that, here, i refers to
an index into the row-major format for the multi-dimensional array,
rather than an index in any particular dimension.
out, ostride and odist describe the output array(s).
The format is the same as for the input array.
FFTW_IN_PLACE option.
The function fftwnd_one transforms a single, contiguous input
array to a contiguous output array. By definition, the call
fftwnd_one(plan, in, out)
is equivalent to
fftwnd(plan, 1, in, 1, 0, out, 1, 0)
#include <fftw.h> void fftwnd_destroy_plan(fftwnd_plan plan);
The function fftwnd_destroy_plan frees the plan plan
and releases all the memory associated with it. After destruction,
a plan is no longer valid.
The conventions that we follow for the multi-dimensional transform are analogous to those for the one-dimensional transform. In particular, the forward transform has a negative sign in the exponent and neither the forward nor the backward transforms will perform any normalization. Computing the backward transform of the forward transform will multiply the array by the product of its dimensions. The output is in-order, and the zeroth element of the output is the amplitude of the zero frequency component. The Gods forbade using HTML to display mathematical formulas. Please see the TeX or Postscript version of this manual for the proper definition of the n-dimensional Fourier transform that FFTW uses. For completeness, we include a bitmap of the TeX output below:

The one-dimensional real routines are generally prefixed with
rfftw_. (4) Programs using RFFTW
should be linked with -lrfftw -lfftw -lm on Unix systems, or with
the RFFTW, the FFTW, and the standard math libraries in general.
#include <rfftw.h> rfftw_plan rfftw_create_plan(int n, fftw_direction dir, int flags); rfftw_plan rfftw_create_plan_specific(int n, fftw_direction dir, int flags, fftw_real *in, int istride, fftw_real *out, int ostride);
The function rfftw_create_plan creates a plan, which is a data
structure containing all the information that rfftw needs in
order to compute the 1D real Fourier transform. You can create as many
plans as you need, but only one plan for a given array size is required
(a plan can be reused many times).
rfftw_create_plan returns a valid plan, or NULL if, for
some reason, the plan can't be created. In the default installation,
this cannot happen, but it is possible to configure RFFTW in such a way
that some input sizes are forbidden, and RFFTW cannot create a plan.
The rfftw_create_plan_specific variant takes as additional
arguments specific input/output arrays and their strides. For the last
four arguments, you should pass the arrays and strides that you will
eventually be passing to rfftw. The resulting plans will be
optimized for those arrays and strides, although they may be used on
other arrays as well. Note: the contents of the in and out arrays are
destroyed by the specific planner (the initial contents are
ignored, so the arrays need not have been initialized).
See Section Discussion on Specific Plans, for a discussion on specific plans.
n is the size of the transform. It can be
any positive integer.
dir is the direction of the desired transform, either
FFTW_REAL_TO_COMPLEX or FFTW_COMPLEX_TO_REAL,
corresponding to FFTW_FORWARD or FFTW_BACKWARD,
respectively.
flags is a boolean OR (`|') of zero or more of the following:
FFTW_MEASURE: this flag tells RFFTW to find the optimal plan by
actually computing several FFTs and measuring their
execution time. Depending on the installation, this can take some
time.
FFTW_ESTIMATE: do not run any FFT and provide a "reasonable"
plan (for a RISC processor with many registers). If neither
FFTW_ESTIMATE nor FFTW_MEASURE is provided, the default is
FFTW_ESTIMATE.
FFTW_OUT_OF_PLACE: produce a plan assuming that the input
and output arrays will be distinct (this is the default).
FFTW_IN_PLACE: produce a plan assuming that you want the output
in the input array. The algorithm used is not necessarily in place:
RFFTW is able to compute true in-place transforms only for small values
of n. If RFFTW is not able to compute the transform in-place, it
will allocate a temporary array (unless you provide one yourself),
compute the transform out of place, and copy the result back.
Warning: This option changes the meaning of some parameters of
rfftw (see Section Computing the Real One-dimensional Transform).
The default mode of operation is FFTW_OUT_OF_PLACE.
FFTW_USE_WISDOM: use any wisdom that is available to help
in the creation of the plan. (See Section Words of Wisdom.)
This can greatly speed the creation of plans, especially with the
FFTW_MEASURE option. FFTW_ESTIMATE plans can also take
advantage of wisdom to produce a more optimal plan (based on past
measurements) than the estimation heuristic would normally
generate. When the FFTW_MEASURE option is used, new wisdom
will also be generated if the current transform size is not completely
understood by existing wisdom.
in, out, istride, ostride (only for
rfftw_create_plan_specific): see corresponding arguments in the
description of rfftw. (See Section Computing the Real One-dimensional Transform.) In particular, the out and
ostride parameters have the same special meaning for
FFTW_IN_PLACE transforms as they have for rfftw.
#include <rfftw.h>
void rfftw(rfftw_plan plan, int howmany,
fftw_real *in, int istride, int idist,
fftw_real *out, int ostride, int odist);
void rfftw_one(rfftw_plan plan, fftw_real *in, fftw_real *out);
The function rfftw computes the Real One-dimensional Fourier
Transform, using a plan created by rfftw_create_plan
(see Section Plan Creation for Real One-dimensional Transforms). The function rfftw_one provides a simplified
interface for the common case of single input array of stride 1.
Important: When invoked for an out-of-place,
FFTW_COMPLEX_TO_REAL transform, the input array is overwritten
with scratch values by these routines. The input array is not modified
for FFTW_REAL_TO_COMPLEX transforms.
plan is the plan created by rfftw_create_plan
(see Section Plan Creation for Real One-dimensional Transforms).
howmany is the number of transforms rfftw will compute.
It is faster to tell RFFTW to compute many transforms, instead of
simply calling rfftw many times.
in, istride and idist describe the input array(s).
There are two cases. If the plan defines a
FFTW_REAL_TO_COMPLEX transform, in is a real array.
Otherwise, for FFTW_COMPLEX_TO_REAL transforms, in is a
halfcomplex array whose contents will be destroyed.
out, ostride and odist describe the output
array(s), and have the same meaning as the corresponding parameters for
the input array.
plan specifies an in-place transform, ostride and
odist are always ignored. If out is NULL,
out is ignored, too. Otherwise, out is interpreted as a
pointer to an array of n complex numbers, that FFTW will use as
temporary space to perform the in-place computation. out is used
as scratch space and its contents destroyed. In this case, out
must be an ordinary array whose elements are contiguous in memory (no
striding).
The function rfftw_one transforms a single, contiguous input array
to a contiguous output array. By definition, the call
rfftw_one(plan, in, out)
is equivalent to
rfftw(plan, 1, in, 1, 0, out, 1, 0)
#include <rfftw.h> void rfftw_destroy_plan(rfftw_plan plan);
The function rfftw_destroy_plan frees the plan plan and
releases all the memory associated with it. After destruction, a plan
is no longer valid.
In this section, we define precisely what RFFTW computes.
The real to complex (FFTW_REAL_TO_COMPLEX) transform of a real
array X of size n computes an hermitian array Y,
where

The complex to real (FFTW_COMPLEX_TO_REAL) transform of a hermitian
array X of size n computes a real array Y, where
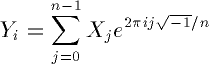
Like FFTW, RFFTW computes an unnormalized transform. In other words, applying the real to complex (forward) and then the complex to real (backward) transform will multiply the input by n.
The multi-dimensional real routines are generally prefixed with
rfftwnd_. Programs using RFFTWND should be linked with
-lrfftw -lfftw -lm on Unix systems, or with the FFTW, RFFTW, and
standard math libraries in general.
#include <rfftw.h>
rfftwnd_plan rfftwnd_create_plan(int rank, const int *n,
fftw_direction dir, int flags);
rfftwnd_plan rfftw2d_create_plan(int nx, int ny,
fftw_direction dir, int flags);
rfftwnd_plan rfftw3d_create_plan(int nx, int ny, int nz,
fftw_direction dir, int flags);
The function rfftwnd_create_plan creates a plan, which is a data
structure containing all the information that rfftwnd needs in
order to compute a multi-dimensional real Fourier transform. You can
create as many plans as you need, but only one plan for a given array
size is required (a plan can be reused many times). The functions
rfftw2d_create_plan and rfftw3d_create_plan are optional,
alternative interfaces to rfftwnd_create_plan for two and three
dimensions, respectively.
rfftwnd_create_plan returns a valid plan, or NULL if, for
some reason, the plan can't be created. This can happen if the
arguments are invalid in some way (e.g. if rank < 0).
rank is the dimensionality of the arrays to be transformed. It
can be any non-negative integer.
n is a pointer to an array of rank integers, giving the
size of each dimension of the arrays to be transformed. Note that these
are always the dimensions of the real arrays; the complex arrays
have different dimensions (see Section Array Dimensions for Real Multi-dimensional Transforms). These sizes, which must be positive
integers, correspond to the dimensions of row-major
arrays--i.e. n[0] is the size of the dimension whose indices
vary most slowly, and so on. (See Section Multi-dimensional Array Format, for
more information.)
nx and ny in rfftw2d_create_plan are positive
integers specifying the dimensions of the rank 2 array to be
transformed. i.e. they specify that the transform will operate on
nx x ny arrays in row-major order, where nx is the number
of rows and ny is the number of columns.
nx, ny and nz in rfftw3d_create_plan are
positive integers specifying the dimensions of the rank 3 array to be
transformed. i.e. they specify that the transform will operate on
nx x ny x nz arrays in row-major order.
dir is the direction of the desired transform, either
FFTW_REAL_TO_COMPLEX or FFTW_COMPLEX_TO_REAL,
corresponding to FFTW_FORWARD or FFTW_BACKWARD,
respectively.
flags is a boolean OR (`|') of zero or more of the following:
FFTW_MEASURE: this flag tells FFTW to find the optimal plan by
actually computing several FFTs and measuring their execution
time.
FFTW_ESTIMATE: do not run any FFT and provide a "reasonable"
plan (for a RISC processor with many registers). If neither
FFTW_ESTIMATE nor FFTW_MEASURE is provided, the default is
FFTW_ESTIMATE.
FFTW_OUT_OF_PLACE: produce a plan assuming that the input
and output arrays will be distinct (this is the default).
FFTW_IN_PLACE: produce a plan assuming that you want to perform
the transform in-place. (Unlike the one-dimensional transform, this
"really" performs the transform in-place.) Note that, if you want to
perform in-place transforms, you must use a plan created with
this option. The use of this option has important implications for the
size of the input/output array (see Section Computing the Real Multi-dimensional Transform).
The default mode of operation is FFTW_OUT_OF_PLACE.
FFTW_USE_WISDOM: use any wisdom that is available to help
in the creation of the plan. (See Section Words of Wisdom.) This can greatly
speed the creation of plans, especially with the FFTW_MEASURE
option. FFTW_ESTIMATE plans can also take advantage of
wisdom to produce a more optimal plan (based on past
measurements) than the estimation heuristic would normally
generate. When the FFTW_MEASURE option is used, new wisdom
will also be generated if the current transform size is not completely
understood by existing wisdom. Note that the same wisdom
is shared between one-dimensional and multi-dimensional transforms.
#include <rfftw.h>
void rfftwnd_real_to_complex(rfftwnd_plan plan, int howmany,
fftw_real *in, int istride, int idist,
fftw_complex *out, int ostride, int odist);
void rfftwnd_complex_to_real(rfftwnd_plan plan, int howmany,
fftw_complex *in, int istride, int idist,
fftw_real *out, int ostride, int odist);
void rfftwnd_one_real_to_complex(rfftwnd_plan p, fftw_real *in,
fftw_complex *out);
void rfftwnd_one_complex_to_real(rfftwnd_plan p, fftw_complex *in,
fftw_real *out);
These functions compute the real multi-dimensional Fourier Transform,
using a plan created by rfftwnd_create_plan
(see Section Plan Creation for Real Multi-dimensional Transforms). (Note that the plan determines the rank and dimensions of
the array to be transformed.) The `rfftwnd_one_' functions
provide a simplified interface for the common case of single input array
of stride 1. Unlike other transform routines in FFTW, we here use
separate functions for the two directions of the transform in order to
correctly express the datatypes of the parameters.
Important: When invoked for an out-of-place,
FFTW_COMPLEX_TO_REAL transform with rank > 1, the input
array is overwritten with scratch values by these routines. The input
array is not modified for FFTW_REAL_TO_COMPLEX transforms or for
FFTW_COMPLEX_TO_REAL with rank == 1.
plan is the plan created by rfftwnd_create_plan.
(see Section Plan Creation for Real Multi-dimensional Transforms). In the case of two and three-dimensional transforms, it
could also have been created by rfftw2d_create_plan or
rfftw3d_create_plan, respectively.
FFTW_REAL_TO_COMPLEX plans must be used with the
`real_to_complex' functions, and FFTW_COMPLEX_TO_REAL
plans must be used with the `complex_to_real' functions. It
is an error to mismatch the plan direction and the transform function.
howmany is the number of transforms to be computed.
in, istride and idist describe the input array(s).
There are howmany input arrays; the first one is pointed to by
in, the second one is pointed to by in + idist, and so on,
up to in + (howmany - 1) * idist. Each input array is stored in
row-major format (see Section Multi-dimensional Array Format), and is not
necessarily contiguous in memory. Specifically, in[0] is the
first element of the first array, in[istride] is the second
element of the first array, and so on. In general, the i-th
element of the j-th input array will be in position in[i *
istride + j * idist]. Note that, here, i refers to an index into
the row-major format for the multi-dimensional array, rather than an
index in any particular dimension.
The dimensions of the arrays are different for real and complex data,
and are discussed in more detail below (see Section Array Dimensions for Real Multi-dimensional Transforms).
FFTW_IN_PLACE option, the transform is
computed in-place--the output is returned in the in array. The
meaning of the stride and dist parameters in this case is
subtle and is discussed below (see Section Strides in In-place RFFTWND).
out, ostride and odist describe the output
array(s). The format is the same as that for the input array. See
below for a discussion of the dimensions of the output array for real
and complex data.
FFTW_IN_PLACE option.
The function rfftwnd_one transforms a single, contiguous input
array to a contiguous output array. By definition, the call
rfftwnd_one_...(plan, in, out)
is equivalent to
rfftwnd_...(plan, 1, in, 1, 0, out, 1, 0)
The output of a multi-dimensional transform of real data contains
symmetries that, in principle, make half of the outputs redundant
(see Section What RFFTWND Really Computes). In practice, it is not
possible to entirely realize these savings in an efficient and
understandable format. Instead, the output of the rfftwnd transforms is
slightly over half of the output of the corresponding complex
transform. We do not "pack" the data in any way, but store it as an
ordinary array of fftw_complex values. In fact, this data is
simply a subsection of what would be the array in the corresponding
complex transform.
Specifically, for a real transform of dimensions
n1 x n2 x ... x nd,
the complex data is an
n1 x n2 x ... x (nd/2+1)
array of fftw_complex values in row-major order (with the
division rounded down). That is, we only store the lower half (plus one
element) of the last dimension of the data from the ordinary complex
transform. (We could have instead taken half of any other dimension,
but implementation turns out to be simpler if the last, contiguous,
dimension is used.)
Since the complex data is slightly larger than the real data, some
complications arise for in-place transforms. In this case, the final
dimension of the real data must be padded with extra values to
accommodate the size of the complex data--two extra if the last
dimension is even and one if it is odd. That is, the last dimension of
the real data must physically contain
2 * (nd/2+1)
fftw_real values (exactly enough to hold the complex data).
This physical array size does not, however, change the logical
array size--only
nd
values are actually stored in the last dimension, and
nd
is the last dimension passed to rfftwnd_create_plan.
The fact that the input and output datatypes are different for rfftwnd
complicates the meaning of the stride and dist parameters
of in-place transforms--are they in units of fftw_real or
fftw_complex elements? When reading the input, they are
interpreted in units of the datatype of the input data. When writing
the output, the istride and idist are translated to the
output datatype's "units" in one of two ways, corresponding to the two
most common situations in which stride and dist parameters
are useful. Below, we refer to these "translated" parameters as
ostride_t and odist_t. (Note that these are computed
internally by rfftwnd; the actual ostride and odist
parameters are ignored for in-place transforms.)
First, there is the case where you are transforming a number of
contiguous arrays located one after another in memory. In this
situation, istride is 1 and idist is the product of
the physical dimensions of the array. ostride_t and
odist_t are then chosen so that the output arrays are contiguous
and lie on top of the input arrays. ostride_t is therefore
1. For a real-to-complex transform, odist_t is
idist/2; for a complex-to-real transform, odist_t is
idist*2.
The second case is when you have an array in which each element has
nc components (e.g. a structure with nc numeric fields),
and you want to transform all of the components at once. Here,
istride is nc and idist is 1. For this
case, it is natural to want the output to also have nc
consecutive components, now of the output data type; this is exactly
what rfftwnd does. Specifically, it uses an ostride_t equal to
istride, and an odist_t of 1. (Astute readers will
realize that some extra buffer space is required in order to perform
such a transform; this is handled automatically by rfftwnd.)
The general rule is as follows. ostride_t equals istride.
If idist is 1 and idist is less than
istride, then odist_t is 1. Otherwise, for a
real-to-complex transform odist_t is idist/2 and for a
complex-to-real transform odist_t is idist*2.
#include <rfftw.h> void rfftwnd_destroy_plan(rfftwnd_plan plan);
The function rfftwnd_destroy_plan frees the plan plan
and releases all the memory associated with it. After destruction,
a plan is no longer valid.
The conventions that we follow for the real multi-dimensional transform are analogous to those for the complex multi-dimensional transform. In particular, the forward transform has a negative sign in the exponent and neither the forward nor the backward transforms will perform any normalization. Computing the backward transform of the forward transform will multiply the array by the product of its dimensions (that is, the logical dimensions of the real data). The forward transform is real-to-complex and the backward transform is complex-to-real.
The Gods forbade using HTML to display mathematical formulas. Please see the TeX or Postscript version of this manual for the proper definition of the n-dimensional real Fourier transform that RFFTW uses. For completeness, we include a bitmap of the TeX output below:

#include <fftw.h> void fftw_export_wisdom(void (*emitter)(char c, void *), void *data); void fftw_export_wisdom_to_file(FILE *output_file); char *fftw_export_wisdom_to_string(void);
These functions allow you to export all currently accumulated
wisdom in a form from which it can be later imported and
restored, even during a separate run of the program. (See Section Words of Wisdom.) The current store of wisdom is not
affected by calling any of these routines.
fftw_export_wisdom exports the wisdom to any output
medium, as specified by the callback function
emitter. emitter is a putc-like function that
writes the character c to some output; its second parameter is
the data pointer passed to fftw_export_wisdom. For
convenience, the following two "wrapper" routines are provided:
fftw_export_wisdom_to_file writes the wisdom to the
current position in output_file, which should be open with write
permission. Upon exit, the file remains open and is positioned at the
end of the wisdom data.
fftw_export_wisdom_to_string returns a pointer to a
NULL-terminated string holding the wisdom data. This
string is dynamically allocated, and it is the responsibility of the
caller to deallocate it with fftw_free when it is no longer
needed.
All of these routines export the wisdom in the same format, which we will not document here except to say that it is LISP-like ASCII text that is insensitive to white space.
#include <fftw.h> fftw_status fftw_import_wisdom(int (*get_input)(void *), void *data); fftw_status fftw_import_wisdom_from_file(FILE *input_file); fftw_status fftw_import_wisdom_from_string(const char *input_string);
These functions import wisdom into a program from data stored by
the fftw_export_wisdom functions above. (See Section Words of Wisdom.)
The imported wisdom supplements rather than replaces any
wisdom already accumulated by the running program (except when
there is conflicting wisdom, in which case the existing wisdom is
replaced).
fftw_import_wisdom imports wisdom from any input medium,
as specified by the callback function get_input. get_input
is a getc-like function that returns the next character in the
input; its parameter is the data pointer passed to
fftw_import_wisdom. If the end of the input data is reached
(which should never happen for valid data), it may return either
NULL (ASCII 0) or EOF (as defined in <stdio.h>).
For convenience, the following two "wrapper" routines are provided:
fftw_import_wisdom_from_file reads wisdom from the
current position in input_file, which should be open with read
permission. Upon exit, the file remains open and is positioned at the
end of the wisdom data.
fftw_import_wisdom_from_string reads wisdom from the
NULL-terminated string input_string.
The return value of these routines is FFTW_SUCCESS if the wisdom
was read successfully, and FFTW_FAILURE otherwise. Note that, in
all of these functions, any data in the input stream past the end of the
wisdom data is simply ignored (it is not even read if the
wisdom data is well-formed).
#include <fftw.h> void fftw_forget_wisdom(void);
Calling fftw_forget_wisdom causes all accumulated wisdom
to be discarded and its associated memory to be freed. (New
wisdom can still be gathered subsequently, however.)
#include <fftw.h> void *(*fftw_malloc_hook) (size_t n); void (*fftw_free_hook) (void *p);
Whenever it has to allocate and release memory, FFTW ordinarily calls
malloc and free.
If malloc fails, FFTW prints an error message and exits. This
behavior may be undesirable in some applications. Also, special
memory-handling functions may be necessary in certain
environments. Consequently, FFTW provides means by which you can install
your own memory allocator and take whatever error-correcting action you
find appropriate. The variables fftw_malloc_hook and
fftw_free_hook are pointers to functions, and they are normally
NULL. If you set those variables to point to other functions,
then FFTW will use your routines instead of malloc and
free. fftw_malloc_hook must point to a malloc-like
function, and fftw_free_hook must point to a free-like
function.
Users writing multi-threaded programs must concern themselves with the
thread safety of the libraries they use--that is, whether it is
safe to call routines in parallel from multiple threads. FFTW can be
used in such an environment, but some care must be taken because certain
parts of FFTW use private global variables to share data between calls.
In particular, the plan-creation functions share trigonometric tables
and accumulated wisdom. (Users should note that these comments
only apply to programs using shared-memory threads. Parallelism using
MPI or forked processes involves a separate address-space and global
variables for each process, and is not susceptible to problems of this
sort.)
The central restriction of FFTW is that it is not safe to create
multiple plans in parallel. You must either create all of your plans
from a single thread, or instead use a semaphore, mutex, or other
mechanism to ensure that different threads don't attempt to create plans
at the same time. The same restriction also holds for destruction of
plans and importing/forgetting wisdom. Once created, a plan may
safely be used in any thread.
The actual transform routines in FFTW (fftw_one, etcetera) are
re-entrant and thread-safe, so it is fine to call them simultaneously
from multiple threads. Another question arises, however--is it safe to
use the same plan for multiple transforms in parallel? (It would
be unsafe if, for example, the plan were modified in some way by the
transform.) We address this question by defining an additional planner
flag, FFTW_THREADSAFE.
When included in the flags for any of the plan-creation routines,
FFTW_THREADSAFE guarantees that the resulting plan will be
read-only and safe to use in parallel by multiple threads.
Go to the first, previous, next, last section, table of contents.