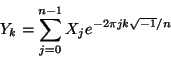 .
.Next: 1d Real-even DFTs (DCTs), Previous: The 1d Discrete Fourier Transform (DFT), Up: What FFTW Really Computes [Contents][Index]
The real-input (r2c) DFT in FFTW computes the forward transform
Y of the size n real array X, exactly as defined
above, i.e.
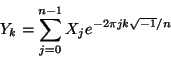 .
.As a result of this symmetry, half of the output Y is redundant (being the complex conjugate of the other half), and so the 1d r2c transforms only output elements 0…n/2 of Y (n/2+1 complex numbers), where the division by 2 is rounded down.
Moreover, the Hermitian symmetry implies that
Y0
and, if n is even, the
Yn/2
element, are purely real. So, for the R2HC r2r transform, the
halfcomplex format does not store the imaginary parts of these elements.
The c2r and H2RC r2r transforms compute the backward DFT of the
complex array X with Hermitian symmetry, stored in the
r2c/R2HC output formats, respectively, where the backward
transform is defined exactly as for the complex case:
 .
.Y of this transform can easily be seen to be purely
real, and are stored as an array of real numbers.
Like FFTW’s complex DFT, these transforms are unnormalized. In other words, applying the real-to-complex (forward) and then the complex-to-real (backward) transform will multiply the input by n.